As the idea of the harmony of the spheres has been anchored in mankind for thousands of years, a coherence between geometry and the celestial relations has also been suspected for an equally long time. Plato associated the five regular solids named after him with the elements of fire, water, earth, air and a celestial-ethereal substance. He attributed the latter to the dodecahedron, a figure, that is enclosed by twelve pentagons. In geometrical regard it was again Johannes Kepler who 2000 years later developed the ancient ideas further. He started out on his search for order in the solar system by creating his well-known model which shows that the arrangement of the six planets, known in his time, is organized by the five Platonic solids. According to this the ratio of the radii of the inner and the outer sphere of the dodecahedron, for example, corresponds (if only very approximately) with that of the mean distances which Mars and Earth have from the Sun, or the semi-major axes of the elliptical orbits, repectively.
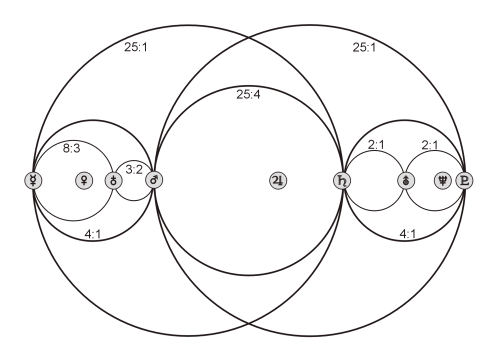
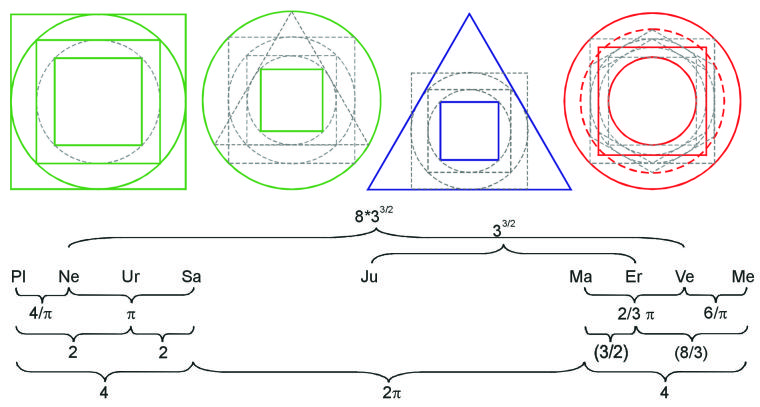
However, the structure of the whole system, as explained in Signature of the Celestial Spheres, is determined by the semi-minor axes b, which already had a central importance in the harmonies of the velocities. What is most striking, is that the first and the fourth planet, counted from the inside as well as from the outside, are in a ratio of 4/1, relative to their semi-minor axes. The first and sixth planet, again calculated from the inside and the outside, show the proportion 25/1. The result is a clear higher structure, that is partitioned further by ratios of small integers. This order is illustrated in the next Figure 4.2 by circles. The differences from the real values amount to only a few thousandths, except for the intervals 8/3 and 3/2, where they are slightly more than one per cent (the exact values can be found in Signature of the Celestial Spheres, page 17).
© Keplerstern Verlag
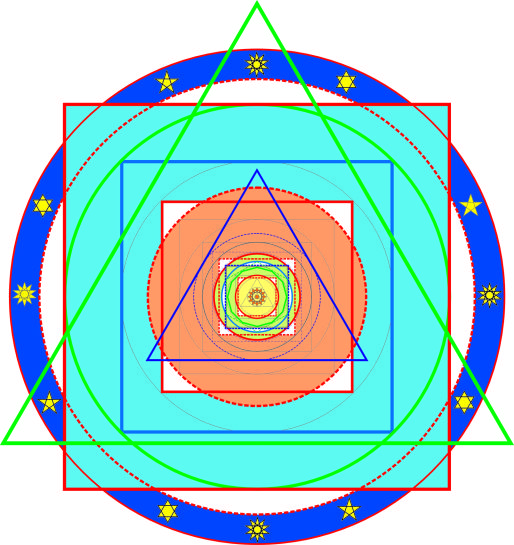
Circle: Neptune
Middle square: Uranus
Inner square: Saturn
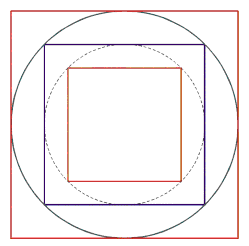
The evolving arrangement is so dazzlingly clear and simple, that we have to wonder once again, why, at least to the authors knowledge, it has not been mentioned anywhere. What we see is something like a reflection in Jupiter, the greatest member of the planetary community, even though Venus and Neptune are not yet integrated into the represented order. We achieve this by using the most simple regular figures: circle, square and triangle. The proportions 2/1 and 4/1 can be derived from the ratios of the areas of the incircle and the circumcircle of a quadrangle respectively a triangle. Thus the circle cuts off proportions in the form 4/p, p/2 etc. As an example we obtain the following arrangement for the four outer planets:
| Planetary relation |
Geometrical relation |
Difference (%) | |
|---|---|---|---|
| Ur/Sa | 2.012 | 2.000 | 0.608 |
| Ne/Ur | 1.568 | 1.571 | 0.156 |
| Pl/Ne | 1.271 | 1.273 | 0.181 |
| Pl/Sa | 4.011 | 4.000 | 0.270 |
Differences between planetary intervals and the
geometrical relations of areas: mean value 0.31%
It may be surprising at first to find three of the orbits as quadrangles. What we are getting at, however, is the representation of the principle behind the distances, i.e. the semi-minor axes. These ratios are like the ratios between areas of squares or circles, repectively. But why do the semi-minor axes play the decisive part in the arrangement of the planetary orbits and why should their proportions be determined by the ratios of areas?
An answer might be found in the fact that the semiminor axes constitute the geometrical mean of the aphelion and the perihelion distances, which makes them the ideal candidate for a geometrical arrangement. If now the measures of distances are determined by relations of areas, Kepler’s laws say – at least as far as circles are concerned – that the velocities correspond approximately to the radii, and the periods of revolution to the spheres constructed with the radii.
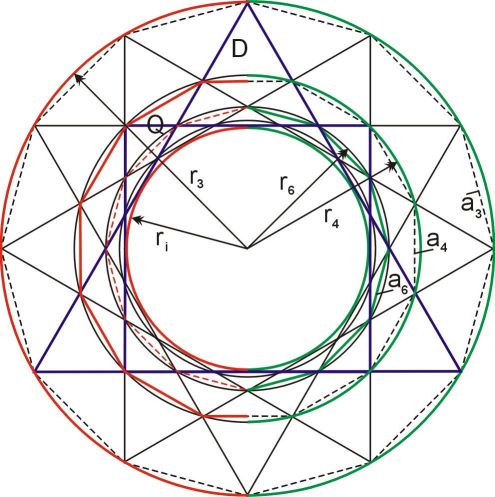
However, we do not intend to propound a new physical theory. Instead we are able to describe very remarkable phenomena. For in a similar fashion we can express all relations of the semiminor axes geometrically (for the inner planetary system we only need the hexagon as an additional tool).
Employing appropriate statistical methods we can show that the likelihood for an accidental occurrence of proportions that result from these simple principles of construction is very small (< 1/100,000). Apart from that it is possible to integrate the Sun (by its diameter) into this kind of representation. But the most astonishing fact is that we find the stated proportions exactly in the ratios of areas, that appear in the twelve-pointed star.
Thus Johannes Kepler’s fundamental idea of a particular order in our solar system, is most beautifully confirmed, even though in a modified way. The more comprehensive intention of his “De Harmonice mundi” (The Harmony of the World), published in 1619, was to point out, that the bases of geometry, musical harmony and astronomy are essentially one, or, in other words, the different spheres of being are interwoven by the same creative principles. What is holding together the world’s interior are for Kepler in the end geometrical prototypes: divine thoughts, which underlie the structure of music and the cosmos. In the human soul they are also anchored as archetypes, enabling us, firstly, to recognize the harmony in the different spheres and to put them into relation.
Circle, square and triangle, then, are the invisible symbols written in the sky which so impressively embody the mysterious order that exists in our solar system. Making our way through the world with open eyes we ever and again discover combinations of these three figures in eloquent symbolism. In scientific modes of thought people link them with the idea of a generally valid and rationally comprehensible cosmic order, while in the religious sense they connect them with the certainty of their faith in a creative force which has ordered the world in ways that will, in the end, make everything turn out for the best. Our celestial home bears these three archetypal images given to us by geometry – and united in the Number of Perfection – as a mark, a signature almost, but perhaps also as a challenge and a promise.– (Signature of the Celestial Spheres, page 292)