The idea of a harmonic order of the cosmos has been a source of inspiration in the history of the human mind for thousands of years. Pythagoras, who as legend has it could hear the music of the spheres, discovered that consonant musical intervals can be expressed in simple ratios of small integers. This concept was transferred by Plato (amongst others) into models about the structure of the universe common in the ancient world. In the early days of the scientific modern age Johannes Kepler gave a fresh impetus to the old ideas, which had been guided by intuition. It was Kepler who laid the foundation for modern conceptions of the harmony of the spheres. Using his own planetary laws he tried to put the traditional ideas on a new, solid foundation. The celestial music, which Kepler tried to find, was to him only perceptible in the mind, i.e. he was trying to find a congruence between musical intervals and planetary relationships.

Johannes Kepler
Fondation St. Thomas, Straßburg
Kepler finally believed he had found these in the extreme angular velocities of the planetary orbits (according to Kepler these are the angles, as seen from the Sun, which the planets cover in identical time intervals). Others after Kepler focussed on other parameters that would fulfil the condition mentioned. For example, Hans Kayser developed a planetary scale from the logarithms of the distances, Thomas Michael Schmidt did the same based on the synodic (related to the earth) periods of revolution – and there were some others. Absent in all efforts to be found in literature is an examination as to whether the concords discovered are significant in terms of probability calculus. In other words, the question has to be asked, whether and how strongly the assumed planetary harmonies differ from a random distribution. Thus, in a series of numerical proportions, which can be derived from parameters such as distance, velocity etc., you will always find several that come close to musical intervals like 2/1, 3/2 etc. To avoid a detailed mathematical discussion a simple graphic immediately illustrates the issue.
Planetary notes calculated from frequencies of the periods of revolution
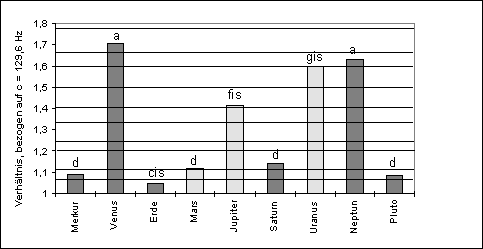
Figure 1.1
Figure 1.1 shows the frequencies – transposed into a single octave -, that are derived from the reciprocal values of the revolution periods (the notes of a planetary scale according to Hans Cousto). The horizontal lines show the musical intervals, and it is obvious, that only 3 out of 9 planetary proportions come anywhere close to the musical ones. Even without further calculation we can see that there is no deviation from a random distribution. Analysing the other celestial harmonies mentioned above the results are essentially no more favourable, not even where Kepler used his angles. But Kepler can be excused in his failure properly to elaborate his basic ideas, because probability calculus was unknown in his time. Furthermore, in his De Harmonice mundi (The Harmony of the World) Kepler explicitly encouraged people to create a system more adequate to the celestial movements than his own.
Thus the analyses mentioned seem to explain why modern astronomy refuses to accept the concept of a harmony of the spheres” (Kepler’s notions concerning these ideas are described in the scientific literature as daydreams or the like. But as yet nobody at least to the author’s knowledge has attempted to include the semi-minor axes in the consideration. At a certain point in time each planet in its revolution around the Sun has exactly the distance of its semi-minor axis b from the central star. The velocity of the planet at this point almost precisely equals the arithmetical mean of the extreme velocities (which occur at aphelion and perihelion, i.e. at the farthest and the nearest points of a planet on its elliptical orbit around the Sun). If we put the velocity at the distances of the semi-minor axes (velocities at b in Figure 1.2) and that at aphelion into correlation, we find a highly significant correspondence with musical intervals.
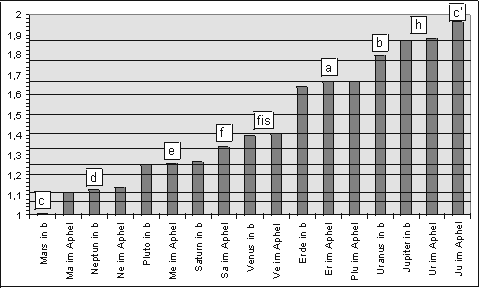
Figure 1.2
Now 13 of 17 possible correlations lie near to or very near to the musical intervals. If we employ statistical methods of calculation, this accumulation can appear only with a probability of 1/10,000 (if we take into account, that there are about 10 possibilities to constitute relations from the different parameters mentioned above, the resulting probability still is only 1/1000). Thus the ancient notion of a harmony of the spheres and especially the fundamental ideas of Johannes Kepler have been confirmed for the first time, and this in a manner that can be verified by anyone. It is not a genuine proof, because this is something which probability calculus will never be able to deliver. Nevertheless we can state in other words, that at the formation of our planetary system there must have been an influence, or force, which with a probability of at least 99.9 % led to an arrangement of orbital velocities that corresponds to the numerical relationships of musical-harmonic intervals.
Figure 1.2 Intervals of velocities, related to Mercury at b as keynote (=c), transposed into a single octave. Musical intervals are marked as horizontal lines.© Keplerstern Verlag
